在幾何學中，正多面體是指各面都是全等的正多邊形且每一個頂點所接的面數都是一樣的多面體。 一般被大眾認知的正多面體通常代表只有五種的凸正多面體，又稱為柏拉圖立體，包括了正四面體、立方體、正八面體、正十二面體和正二十面體。
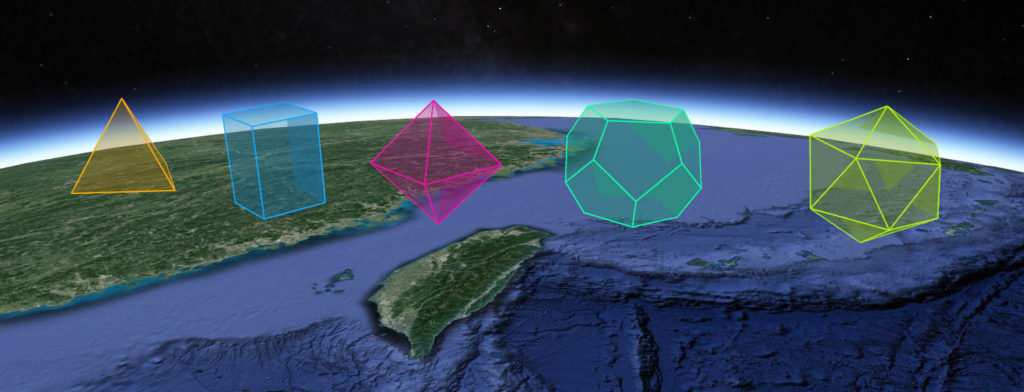
我一直對於幾何學很有興趣，尤其對於這些正多面體如何來計算產生很是好奇，但苦於沒有接觸到一個可以繪出多面體的軟體工具而空想，或者可能曾用過但當時也沒能力來應用，前陣子在作出可以在Google Earth展現 多邊形的變形 之後，我終於跳出Google Earth只能應用在地理上的思維，而把Google Earth當作立體空間的展示工具，繼上一篇彈力球@Google Earth應用在3D立體的變化，接下來當然就是我一直想製作的柏拉圖立體了。
我還是依上一篇 彈力球@Google Earth 的作法，應用 3D極座標的計算式，正四面、立方體、正八面體這三種只要應用簡單三角函數即可計算出，接下來的正十二面體可就碰到挑戰了，苦思了好久，最後還應用上餘弦定理，總算有所突破，接下來的二十面體反而就簡單了。
現在先請大家下載這個正多面體KML
，裡頭前五個網路連結分別可以產生正四面體、立方體、正八面體、正十二面體和正二十面體，第六個網路連結則是產生這五個正多面體的變形。操作方式跟之前幾篇的說明一樣，不過這裡有六個網路連結，第一次使用可先在任一網路連結前打勾即可，之後若改變螢幕範圍則需再用滑鼠右鍵點選各個網路連結，此時會出現一個視窗，選擇”重新整理”即可產生，比如上圖五種多面體同時呈現就是左右移動視窗的應用，好好玩玩吧！
